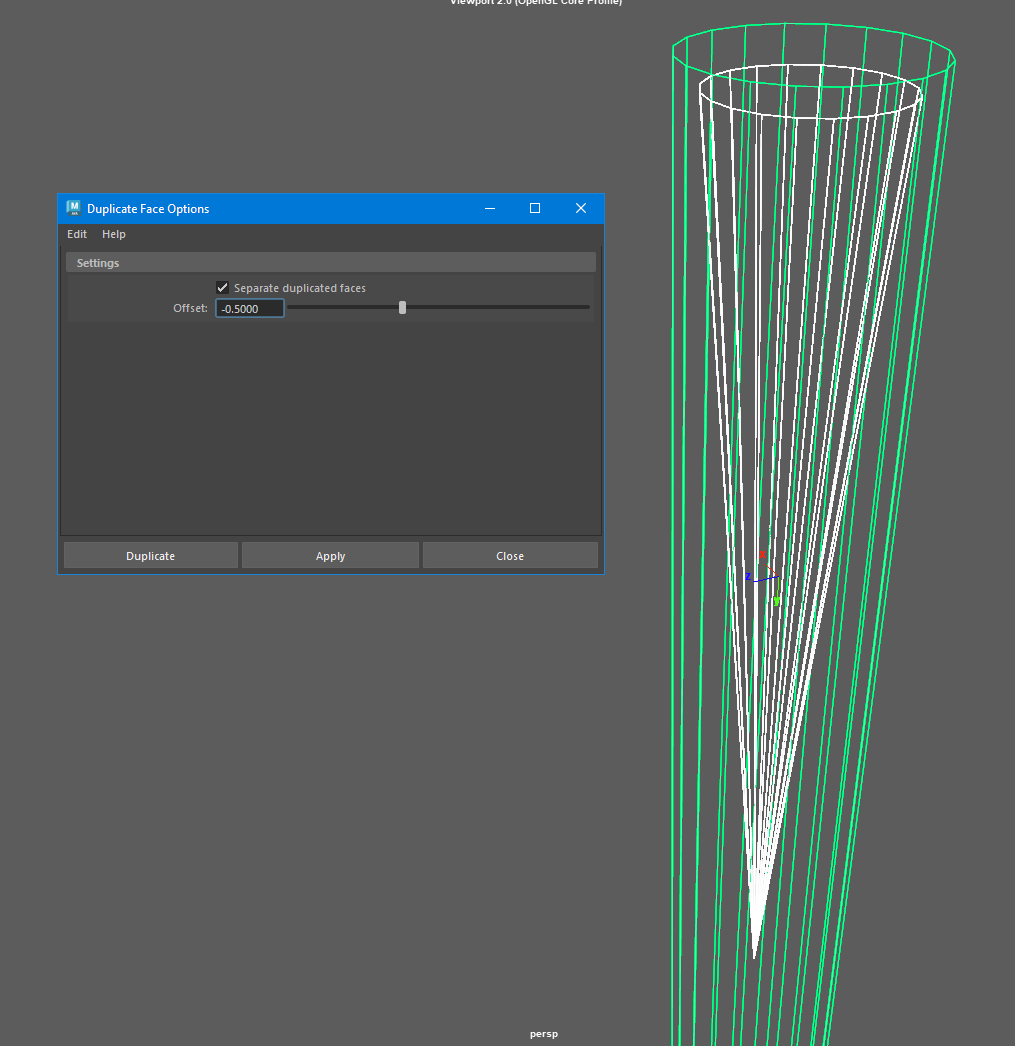
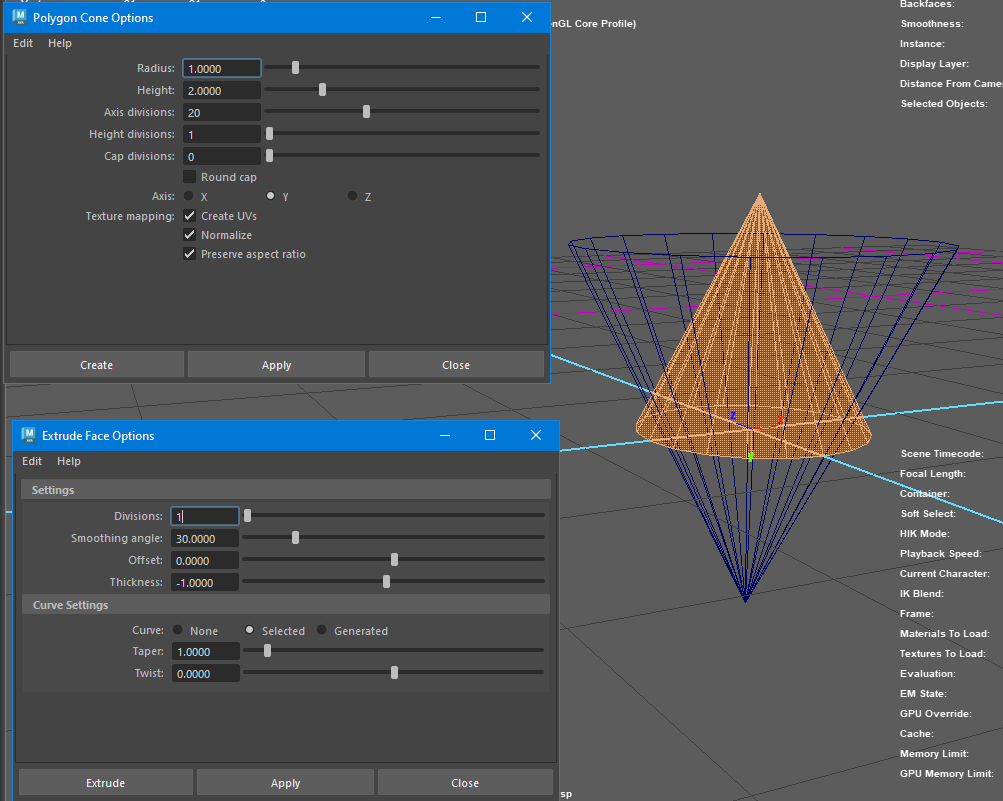
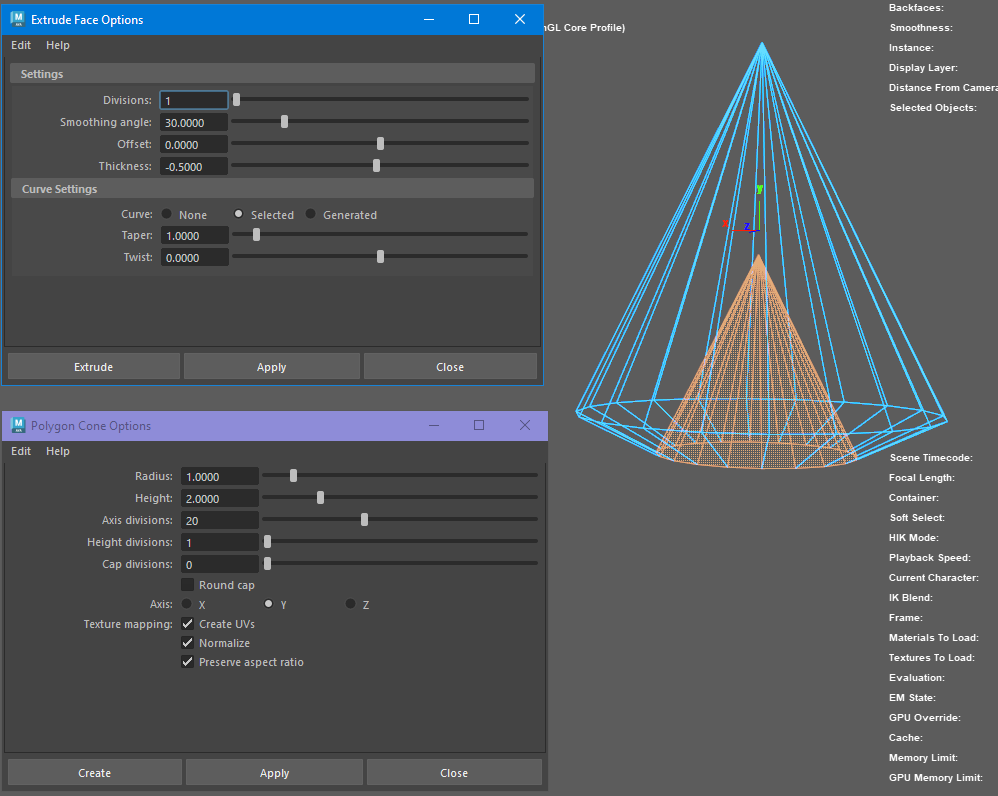
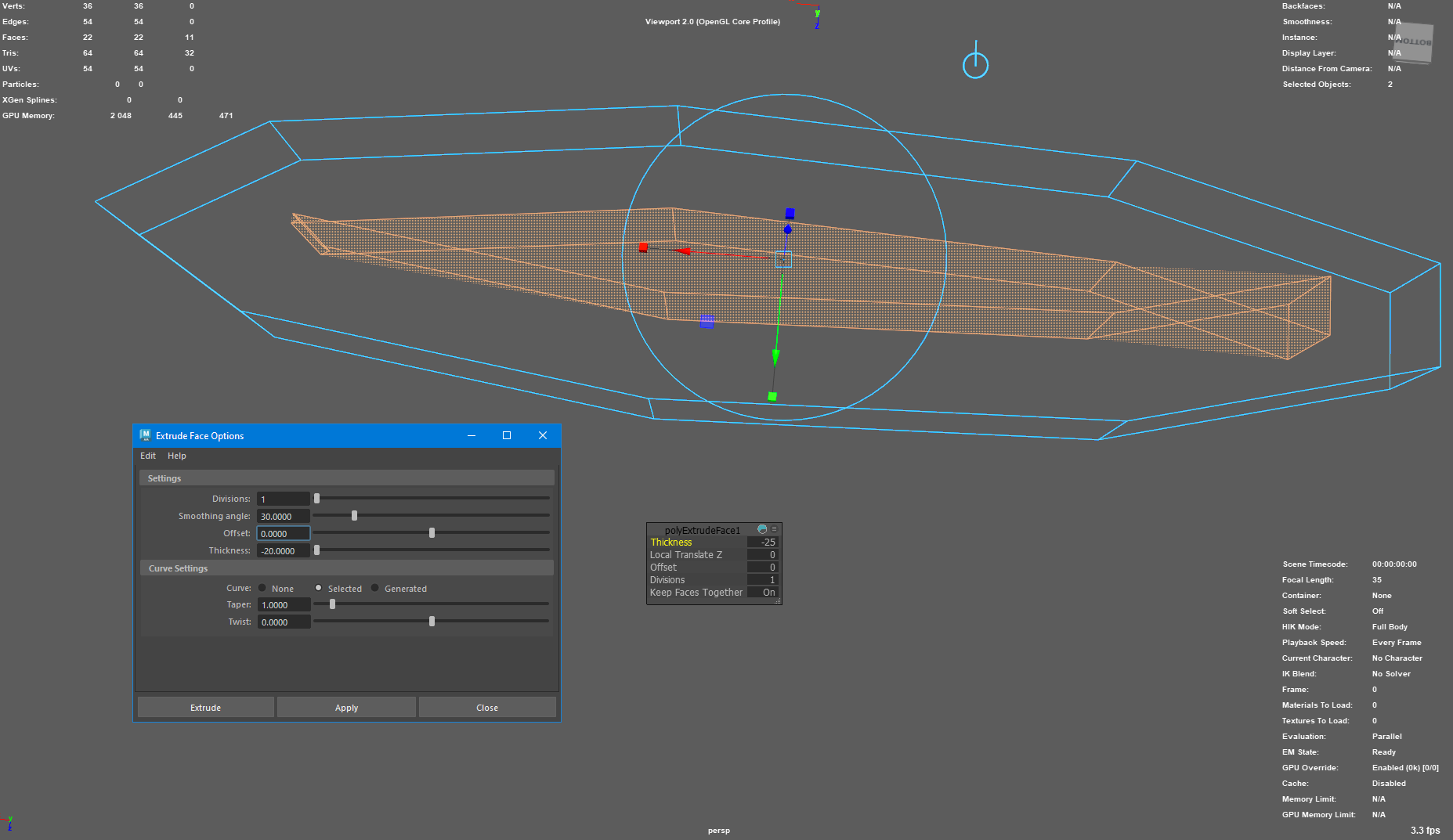
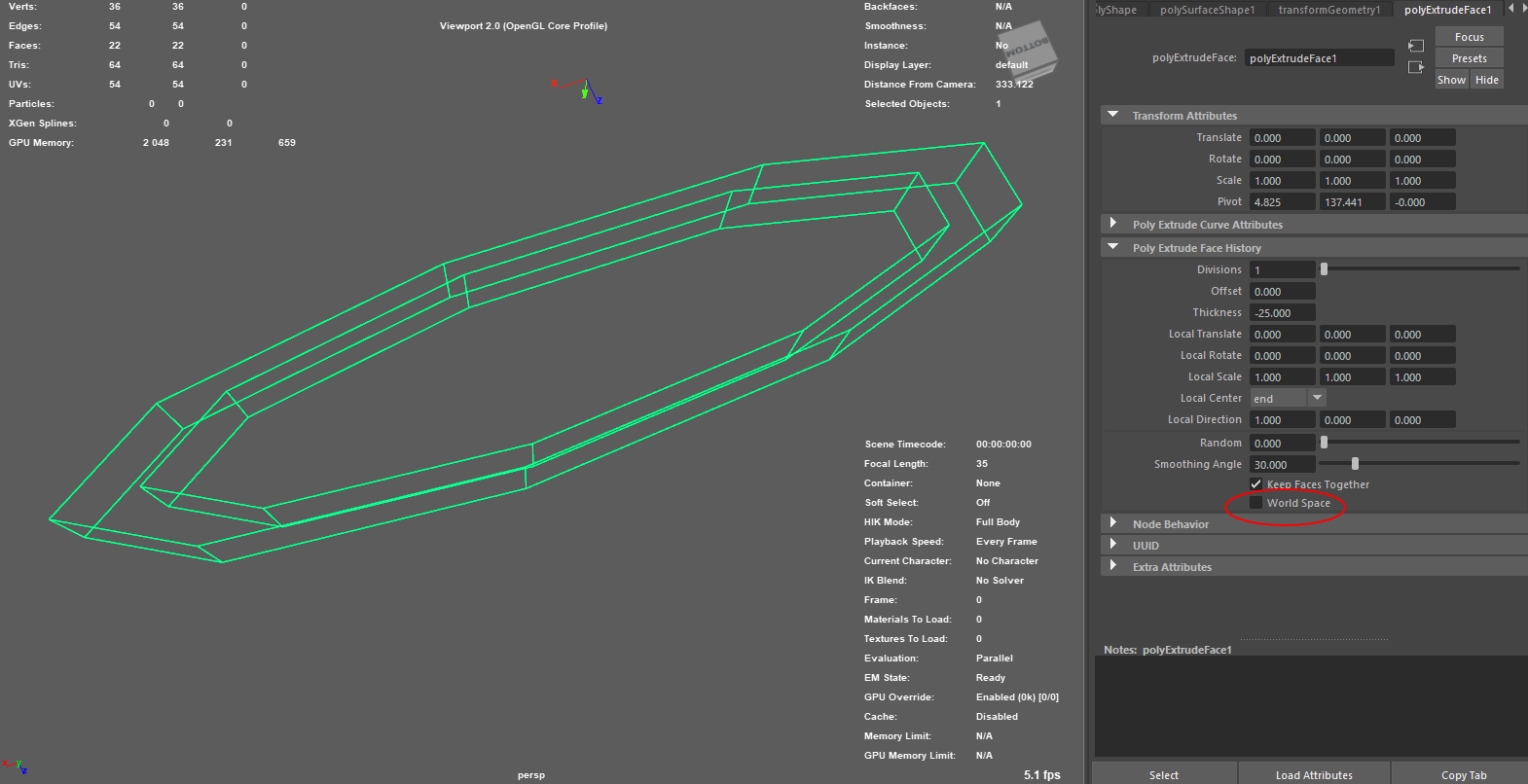
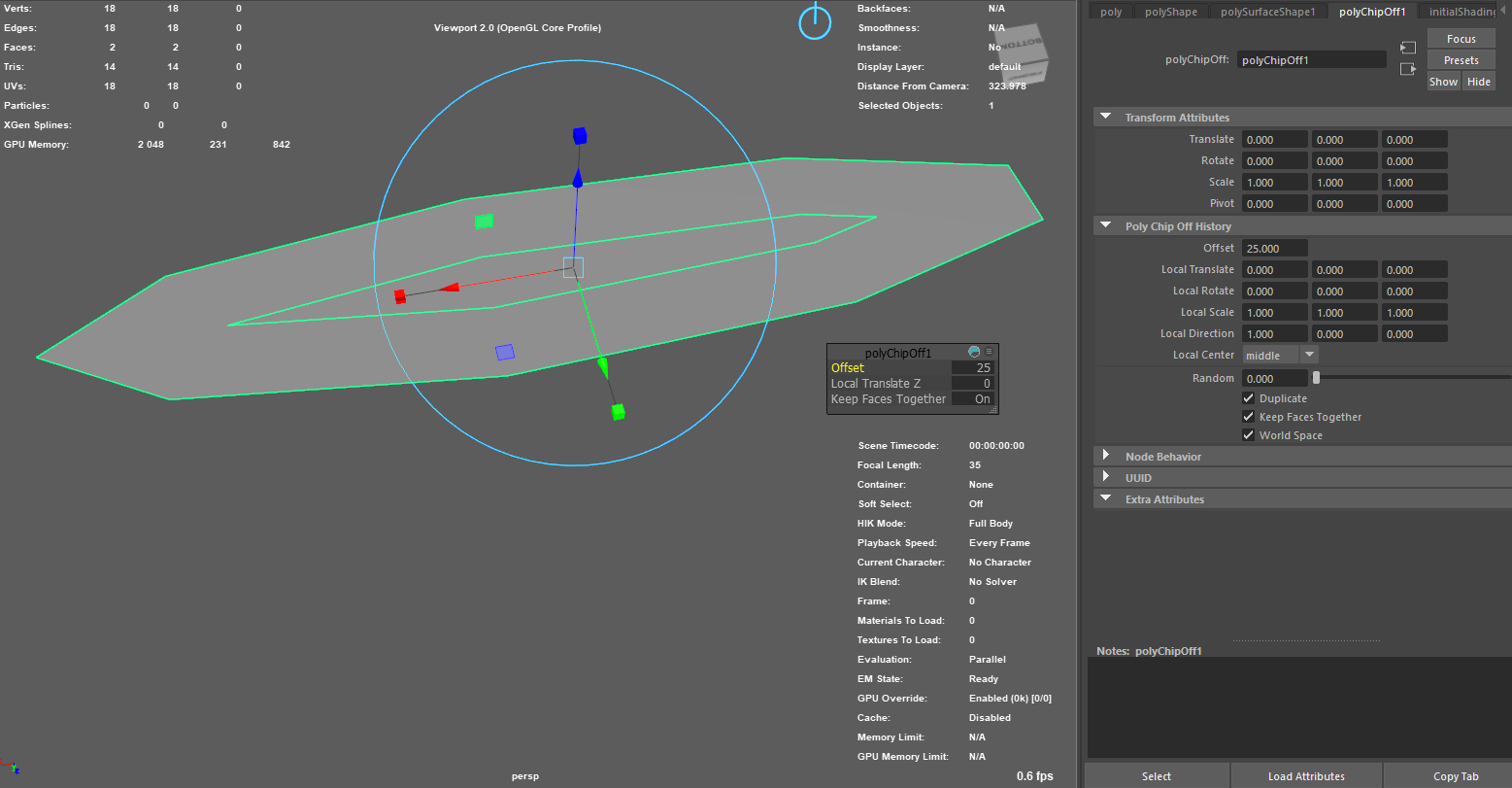
Hi there,
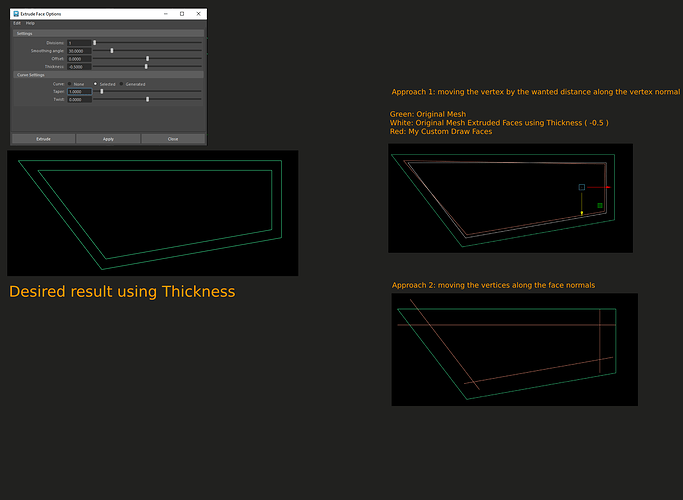
I have a poly mesh where I want to draw an offseted version ( a.k.a thickness ) using MUIDrawManager. The desired result that I am looking for is what Extrude/Thickness in Maya does. When using Thickness, the newly created vertices are displayed uniformly which I want do emulate.
My first approach was to move new vertices along the vertex normal of original mesh but that doesn’t give the uniform displacement.
Pseduo code :
MFnMesh fnMesh(objPath);
std::vector<MPointArray> displacedVertexPositions;
for (int faceIndex = 0; faceIndex < fnMesh.numPolygons(); ++faceIndex) {
// Get the vertex indices for the current face
MIntArray vertexIndices;
fnMesh.getPolygonVertices(faceIndex, vertexIndices);
// Move vertices along the face normal with the specified scale factor
MPointArray faceVertexPositions;
for (unsigned int i = 0; i < vertexIndices.length(); ++i) {
MPoint vertexPosition;
fnMesh.getPoint(vertexIndices[i], vertexPosition, MSpace::kObject);
MVector normal;
fnMesh.getVertexNormal(vertexIndices[i], true, normal, MSpace::kObject);
// Adjust the displacement to account for the desired thickness or scale
MVector displacement = normal * scale;
// Move the vertex along the adjusted displacement
MPoint displacedPoint = vertexPosition + displacement;
faceVertexPositions.append(displacedPoint);
}
displacedVertexPositions.push_back(faceVertexPositions);
}
// draw wireframe mesh
for (const MPointArray& points : displacedVertexPositions) {
drawManager.mesh(MUIDrawManager::kClosedLine, points);
}
For the second approach, I am trying to move the new vertices along the Face center normal. The new vertices are displaced uniformly but not properly connected.
I am trying to figure out what I am missing here and if there is a better way to do this
std::vector<MPointArray> displacedVertexPositions;
for (int faceIndex = 0; faceIndex < numFaces; ++faceIndex) {
// Get the vertex indices for the current face
MIntArray vertexIndices;
fnMesh.getPolygonVertices(faceIndex, vertexIndices);
// Compute the face normal
MFloatVectorArray normals;
fnMesh.getFaceVertexNormals(faceIndex, normals);
MVector centerNormal(0.0, 0.0, 0.0);
for (unsigned int i = 0; i < normals.length(); ++i) {
centerNormal += MVector(normals[i].x, normals[i].y, normals[i].z);
}
centerNormal /= normals.length();
centerNormal.normalize();
MPointArray faceVertexPositions;
for (unsigned int i = 0; i < vertexIndices.length(); ++i) {
MPoint vertexPosition;
fnMesh.getPoint(vertexIndices[i], vertexPosition, MSpace::kObject);
// move vertex position along face center normal
MPoint displacedPoint = vertexPosition + centerNormal * scale;
faceVertexPositions.append(displacedPoint);
}
displacedVertexPositions.push_back(faceVertexPositions);
}
for (const MPointArray& vertPos : displacedVertexPositions) {
drawManager.mesh(MUIDrawManager::kClosedLine, vertPos);
}
Any help is appreciated.