The task you have identified can be divided into two subtasks:
- Creating a certain ellipse with certain parameters
- Creation of spheres, positioning (distribution) of these spheres on the ellipse curve in accordance with the given logic.
The essence of the proposed method is as follows:
An ellipse can be characterized using two parameters: The length of the major semi-axis and the length of the minor semi-axis.
The ratio of the lengths of the small and large pull-axes is called the compression ratio or ellipticity.
As an ellipse, we can create a NURBS Circle (for example, in the XZ plane).
We scale the resulting curve to the ellipse we need (Scale X = Length of the major semiaxis, Scale Z = Length of the minor semiaxis).
Now we have the opportunity to use the built-in NURBS Curve parameters for our own purposes.
NURBS Curves have the property of parameterization.
That is, there is some value, called a parameter, that changes along the length of the curve. UV analogue (U-parameter).
In Maya, a curve can be created with a “Uniform” parameterization type (the value of the parameter increases uniformly from zero to one, or from zero to Curve Num Spans).
Or the curve can be created with the parameterization type “Chord length” (The value of the parameter on the curve is equal to the length of the curve at that location).
We can request the value of a parameter for a certain curve length, and then we can request the coordinates of a point on the curve for that parameter.
A small non-lyrical digression:
If the parameterization on our curve were “Chord length”, then we could immediately request the coordinates for a point on the curve by inserting the length value into the parameter value.
But all NURBS primitives in Maya are created with “Uniform” parameterization…
Without special tricks, we cannot change the parametrization from “Uniform” to “Chord length”.
Yes, but the “Uniform” parameterization is uniform and we can, for example, to find the coordinate of a point located exactly in the middle on the curve (with “Uniform” parameterization 0-1), request the position of the point for the parameter = 0.5?
If we actively change our curve with “Control Vertex/Edit Points”, it will be noticeable to the naked eye that the parametrization becomes NOT UNIFORM! To restore uniform parameterization after any such manipulations, it will be necessary to perform the Uniform Rebuild Curve… operation.
And still, it won’t be very accurate. And it is not at all accurate if there are few control points, and the changes in curvature on the curve are significant and/or the changes in curvature are steep.
So it goes…
MEL (or Python cmds) has a “PointOnCurve” command that can return the position for the specified parameter value.
But, since we intend to request the position of a point on the curve for an arbitrary value of the length of this curve, we will immediately use the Python API.
For our ellipse, let’s introduce an additional parameter “sweep” - the opening angle. The value “360”/"-360" indicates that the curve is closed.
Let’s formulate our requirements:
Create an ellipse with semi-axes of a given length (for example 10 and 20)
Let the opening angle be full (360 degrees)
The center of the ellipse must be at the specified coordinates (e.g. (0.0, 0.0 ,0.0))
The ellipse must be built in the specified plane (for example XZ)
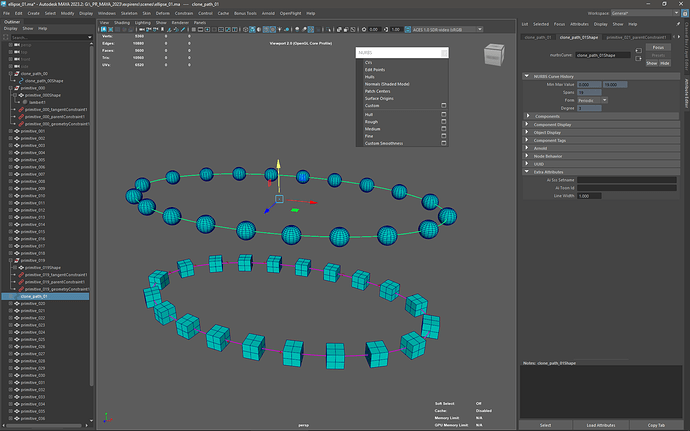
Create the specified number of polygon primitives of a given size (for example, let the number of primitives = 20. For clarity, let these be polygon cubes with a size of 1 x 1 x 1 and subdiv = 2 x 2 x 2)
Evenly distribute primitives along the curve at equal intervals of the length of the curve.
The position of the first primitive must correspond to the start point of the curve, and the position of the last primitive must correspond to the end point of the curve.
In this case, if the position of the first and last points coincide (for example, the curve is closed), then the last primitive should not be in the position of the first primitive.
All primitives, anyway, must be evenly distributed along the curve at regular intervals.
In this case, the curve must pass through the centers of the primitives, and the primitives must be rotated in accordance with the tangent of the curve at this point.
Once created, when moving and transforming the curve (translate, rotate, scale), distributed primitives must maintain their positions on the curve.
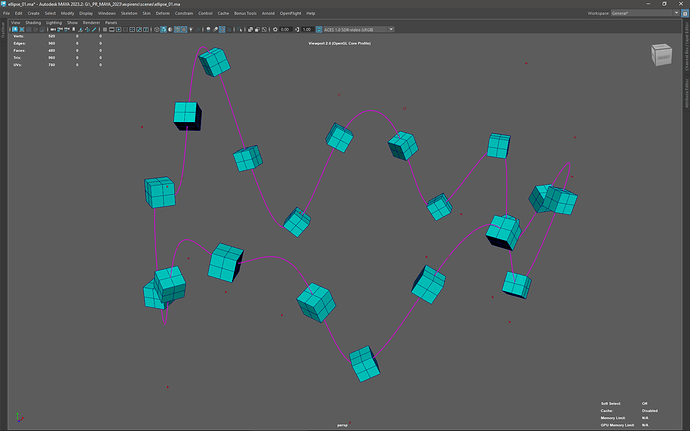
After modifying the curve, for example by changing the position of “Control Vertex/Edit Points”, and/or removing/adding them, provide additional functionality to re-distribute and position primitives on the curve.
So, let’s move on to the code.
import maya.cmds as cmds
import maya.api.OpenMaya as om
# PART I: CREATE ELLIPSE CURVE
# Input parametrs for ellipse
axis_minor = 10.
axis_major = 20.
c_sweep = 360.
c_center = (0., 0. ,0.)
c_name = "clone_path_00"
if c_sweep < -360.0: c_sweep = -360.0
if c_sweep > 360.0: c_sweep = 360.0
# Set number of primitives
primitives = 20
# Input parametrs for circle
c_radius = 1.
c_sections = primitives - 1
c_degree = 3
c_normal = (0., 1., 0.)
c_tolerance = 0.001
# Create circle curve
create_circle = cmds.circle( name = c_name, sweep = c_sweep, radius = c_radius, sections = c_sections, degree = c_degree, center = c_center, normal = c_normal, ch=0)
cmds.select(cl=1)
# For clarity, change the color and thickness of the curve
cmds.setAttr(create_circle[0] + "Shape.overrideEnabled", 1)
cmds.setAttr(create_circle[0] + "Shape.overrideColor", 9)
cmds.setAttr(create_circle[0] + "Shape.lineWidth", 1)
# Let's pass our curve to MFnNurbsCurve
sel = om.MSelectionList()
sel.add(create_circle[0])
dag = sel.getDagPath(0)
dag_shape = dag.extendToShape(0)
mfn_curve = om.MFnNurbsCurve(dag)
# Scale curve for ellipse axis size
cmds.scale(axis_major/2, 1, axis_minor/2, create_circle[0], a=1)
#
# There may be optional code here for aditional curve transformation : scale, rotate, translate ...
#
# Next, you should freeze and reset the transformations of the curve so that the length of this curve is correctly calculated.
cmds.makeIdentity(create_circle, apply = True, t = 1, r = 1, s = 1, n = 0, pn = 1)
cmds.makeIdentity(create_circle, apply = False, t = 1, r = 1, s = 1)
# Let's calculate the length of the curve.
c_length = mfn_curve.length(c_tolerance)
# PART II: Creation and distribution of primitives by ellipse curve parameter
# Set Name for Primitive
s_name = "primitive_000"
# Primitive selector
# "0" for spheres, or "1" for cubes
set_primitive = 1
# Set the values for the input attributes of the sphere primitive creation
s_radius = 0.5
s_subd_axis = 16
s_subd_height = 16
# Set values for the input attributes of creating a primitive cube
cube_w = 1.
cube_h = 1.
cube_d = 1.
cube_sx = 2
cube_sy = 2
cube_sz = 2
cube_ax = (0., 1., 0.)
# Let's create a list in which we will place the names of the created primitives.
primitives_list = []
# Let's create a list in which we will place the names of the created constraints.
constr_list = []
# We organize a cycle for creating and distributing primitives along a curve.
# The essence of the idea is to divide the length of the curve into a given number of spheres
# and place the spheres at these parameter positions.
# Set the number of iterations equal to the number of spheres.
for i in range(primitives):
# number of span for primitives = (primitives - 1) if curve open (mfn_curve.form == 1)
# This can happen if the "sweep" parameter is: -360.0 < sweep > 360.0 (e.g. sweep = 350.0 or sweep = -350.0)
# number of span for primitives = primitives if curve closed/periodic (mfn_curve.form == 2 or 3)
if mfn_curve.form == 1: use_lenght = c_length/(primitives-1)*i
if (mfn_curve.form == 2) or (mfn_curve.form == 3): use_lenght = c_length/(primitives)*i
# Calculate the value of the curve parameter for the specified length
parametr_for_length = mfn_curve.findParamFromLength(use_lenght, c_tolerance)
# Calculate the position of the point for the specified parameter
point_for_parametr = mfn_curve.getPointAtParam(parametr_for_length, 4)
# Create a polygon primitive for a given selection of primitives
if set_primitive == 0:
create_primitive = cmds.polySphere(name = s_name, radius = s_radius, sa = s_subd_axis, sh = s_subd_height, ch = 0)
else:
create_primitive = cmds.polyCube(name = s_name, w = cube_w, h = cube_h, d = cube_d, sx = cube_sx, sy = cube_sy, sz = cube_sz, ax = cube_ax, cuv = 4, ch = 0)
cmds.select(cl=1)
# Move the primitive to the calculated position (point_for_parametr)
cmds.move(point_for_parametr[0], point_for_parametr[1], point_for_parametr[2], create_primitive[0], a=1)
# Let's make the primitive rotate according to the tangent of the curve. Let's apply for this tangent konstrain.
tg_constr = cmds.tangentConstraint(create_circle[0], create_primitive[0], weight = 1.0, aimVector=(1, 0, 0) ,upVector=(0, 1, 0), worldUpType = "vector", worldUpVector=(0, 1, 0))
constr_list.append(tg_constr[0])
# Let's make the primitive behave as if it were a descendant of the curve. Apply for this Parent Constraint
par_const = cmds.parentConstraint(create_circle[0], create_primitive[0], mo = 1, weight = 1.0)
constr_list.append(par_const[0])
# Let's make the primitive fit the modified curve. Apply for this Geometry Constraint
geo_const = cmds.geometryConstraint(create_circle[0], create_primitive[0], weight = 1.0)
constr_list.append(geo_const[0])
primitives_list.append(create_primitive[0])
# So now we can move and rotate the curve.
# In this case, the primitives follow the curve and keep their positions on the curve.
# But, we may want to change the shape of our curve more fundamentally.
# Scale heavily, or change the shape of the curve by changing the position of the "Control Vertex"/"Edit Points",
# and/or removing/adding them.
# PART III: Redistribute Primitives for the Modified Curve
# After every major change to the curve, execute this block of code.
# Delete all the constraints we created in the previous steps.
for item in constr_list:
try: cmds.delete(item)
except: pass
# Let's clean up our list of constraints
constr_list = []
# Further, as in the previous time, it is necessary to freeze and reset the transformations
# of the curve so that the length of this curve is correctly calculated.
cmds.makeIdentity(create_circle[0], apply = True, t = 1, r = 1, s = 1, n = 0, pn = 1)
cmds.makeIdentity(create_circle[0], apply = False, t = 1, r = 1, s = 1)
# Now we calculate again the correct length of the curve with a given accuracy
c_length = mfn_curve.length(c_tolerance)
# In this cycle, everything is arranged the same as last time,
# except that we do not create primitives,
# but use the list of primitives obtained when they were created.
for i in range (len(primitives_list)):
# number of span for primitives = (primitives - 1) if curve open (mfn_curve.form == 1)
# number of span for primitives = primitives if curve closed/periodic (mfn_curve.form == 2 or 3)
if mfn_curve.form == 1: use_lenght = c_length/(primitives-1)*i
if (mfn_curve.form == 2) or (mfn_curve.form == 3): use_lenght = c_length/(primitives)*i
parametr_for_length = mfn_curve.findParamFromLength(use_lenght, c_tolerance)
point_for_parametr = mfn_curve.getPointAtParam(parametr_for_length, 4)
cmds.move(point_for_parametr[0], point_for_parametr[1], point_for_parametr[2], primitives_list[i], a=1)
tg_constr = cmds.tangentConstraint(create_circle[0], primitives_list[i], weight = 1.0, aimVector=(1, 0, 0) ,upVector=(0, 1, 0), worldUpType = "vector", worldUpVector=(0, 1, 0))
constr_list.append(tg_constr[0])
par_const = cmds.parentConstraint(create_circle[0], primitives_list[i], mo = 1, weight = 1.0)
constr_list.append(par_const[0])
geo_const = cmds.geometryConstraint(create_circle[0], primitives_list[i], weight = 1.0)
constr_list.append(geo_const[0])
Please excuse any confusion, English is not my native language…
Good luck!