So I’m writing an importer for our engine skeleton data into Maya (to learn C++ and the Maya API)
the skeleton data is stored as Rotation(xyzw Quaternion), Scale(x,y,z vector) and Translation(x,y,z vector)
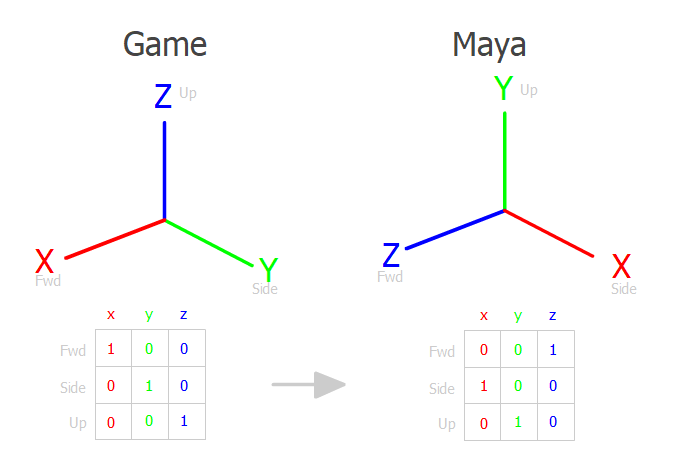
I am confronted by the ubiquitous Z-up vs Y-up conversion.
I solved this ‘brute force’ swapping the xyz components:
/*================================
engine Z up to Maya Y up 4x4 matrix
x y z w
| 0 0 1 0 |
| 1 0 0 0 |
| 0 1 0 0 |
| 0 0 0 1 |
==================================*/
// 'brute force' axis swapping based on the matrix seems to work
void engineToMayaSpaceVector(MVector & v) {
MVector temp;
temp.x = v.y;
temp.y = v.z;
temp.z = v.x;
v = temp;
}
void engineToMayaSpaceQuat(MQuaternion & q) {
MQuaternion temp;
temp.x = q.y;
temp.y = q.z;
temp.z = q.x;
temp.w= q.w;
q= temp;
}
The above code seems to do the trick.
But I believe (correct me if I’m wrong) that this can all be done by a matrix multiplication?
mayaScaleVector = ZtoYupMatrix * engineScaleVector
mayaRotationQuaternion = ZtoYupMatrix * engineRotationQuaternion
mayaTranslateVector = ZtoYupMatrix * engineTranslateVector
When I attempt this I get very incorrect results.
Is my premise wrong, or is my execution flawed?
/*================================
for MMatrix, we need to build a float matrix[4][4]
where the x,y,z,w components are each row (i think)
x y z w
i| 0 0 1 0 |
j| 1 0 0 0 |
k| 0 1 0 0 |
l| 0 0 0 1 |
const float matrix[4][4] ={
xi,xj,xk,xl,
yi,yj,yk,yl,
zi,zk,zj,zl,
wi,wj,wk,wl
}
^^^^^^^^^
(is this the correct way to build the matrix?)
==================================*/
const float ENGINE_TO_MAYA_ARRAY[4][4] = {
0.0, 1.0, 0.0, 0.0,
0.0, 0.0, 1.0, 0.0,
1.0, 0.0, 0.0, 0.0,
0.0, 0.0, 0.0, 1.0
};
const MMatrix ENGINE_TO_MAYA_MATRIX = ENGINE_TO_MAYA_ARRAY;
//convert by matrix multiply
void engineToMayaSpaceVectorMatrix(MVector & v) {
v = ID_TO_MAYA_MATRIX*v;
}
//convert by matrix multiply
void engineToMayaSpaceQuatMatrix(MQuaternion & q) {
q = ID_TO_MAYA_MATRIX*q;
}
), they care more for what the first, second, and third Euler axes are, and will set up their joints with that in mind to avoid gimbal lock.