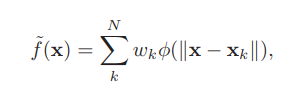Thank you to everyone who’s taken the time to reply to this thread. It’s all been very helpful!
I believe I have an algorithm that, while it does need more stress testing to examine the results, seems to give me what I’m looking for.
For those that want to check into this, here’s where I’m at:
The equation we need is 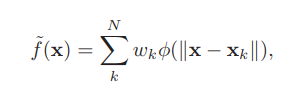
If X in this equation is the driver values we’re trying to find the pose for, then there needs to be some function to run on those driver values that will give us our result. That function assumes we have a set of test data (our set poses) to work with, which in this case is represented by ‘k.’ So for every bit of test data, we need to find the distance between X (our driver values) and that test data. That answer will be run through some other function if desired (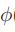 ) and then multiplied by some unknown weight value (‘wk’). All those answers will be added to together and then BAM… that’s the pose you want.
) and then multiplied by some unknown weight value (‘wk’). All those answers will be added to together and then BAM… that’s the pose you want.
The problem is that we don’t know what that ‘wk’ is for each of our test data. That’s what Marcus appears to be trying to solve for initially using Ax = B.
To do this, I’m using scipy’s libraries to handle the heavy lifting. If you run every driver value in your data set through the pdist function to get the complete . I then squareform that result for use in Ax = B. The trick is to remember that we will likely run this distance through a basis function. Whatever function we choose, this distance matrix needs to have it applied prior to solving Ax = B. For reference on what some potential basis functions look like, check out scipy’s Rbf class. While I didn’t use that class specifically, the documentation reference is pretty handy. Also, thankfully, scipy’s functions allow for matrix inputs so if you want to find exponential results you can in one line (i.e. exp, sqrt, power, etc).
From here, scipy comes to the rescue again with solve. This will solve our Ax = B problem that we find in Marcus’ post. If we construct our desired answer, B, with a matrix of all the data sets’ pose values and our A is the result of the distance work we just did and pump it into this ‘solve’ function, we get our weight values (‘wk’). I will say that I’m not sure how Marcus came to that weight matrix he has. Scipy’s results are very different from both his as well as the matrix math site he points to. My only guess is that he is using some sort of basis function to get those numbers but doesn’t reveal which one 
All this information is developing our ‘pose space.’ We now have enough info to solve the RBF function above on our data set with, hopefully, any given test input.
So if X is whatever my input values are, I should now be able to find the distance between it and every driver value in my data set. I run that answer through the exact same basis function I used to solve for the weights and multiply by the given weight. Keep in mind that the weight value in this case is going to be an array of values. For example (if we for a moment just assume Marcus’ matrices are all correct):
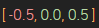 -
- 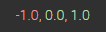
is run through a basis function, then multiplied by 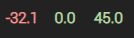
We then do this for every row of starting driver values and add all those result up. Our answer is then the pose values we’re looking for.
I’ve been testing this by trying this process with one of the driver values in the initial data set (-1, 0, 1 for example). If I get the corresponding pose value in the data set as my result, I’m feeling pretty good that I’m doing alright. Part of the usefulness of the RBF approach is that if we’re interpolating through known data points we should be getting our known values.
That’s what I have for now. I’m successfully using a gaussian basis function, but I also am having an issue with multi-quadric and thin-plate functions. I wouldn’t be surprised if I’m missing something. Next as well is to use some sort of ‘decomposition’ to help with Ax = B when A and B are not of similar dimensions.
TLDR: 
 Any help with to clarify or explain the applied math here would be greatly appreciated. Thanks!
Any help with to clarify or explain the applied math here would be greatly appreciated. Thanks!