Hey TA.org,
You guys are awesome. Thanks for all the help.
I just wanted to check if there is an existing function to do this rather than solving this system of equations in python:
If Line A and Line B do not intersect:
Find the points on Line A and Line B respectively that exist at the shortest distance between two curves. (the end points of this new line segment C would be orthogonal to both Line A and B)
As you have it here, this would mean that A and B are parallel – is that your intent? If they aren’t parallel, none of the connecting lines could be orthogonal to both lines… but if they are parallel, all solutions are equally good within the overlap of the two lines, since they’re all equal length.
Hey Theodox,
Apologies if I was unclear… what I meant was these are skewed lines in 3d space. In 2 dimensions, yes, all non parallel lines intersect, but in 3 dimensions lines can be skewed:
In python I would attempt to implement this:
The only functions I know of that are somewhat related but don’t do what I want would be closestPointOnMesh and closestPointOnCurve. But they give me the point on one line that is closest to a point in 3d space.
What I need is the shortest line between two lines in 3d space… was wondering if there is a better function to use to solve for what I wanted.
I had to do a bunch of this at one point in time, and I found this great resource: http://geomalgorithms.com/a07-_distance.html. It includes the derivation of the algorithms, and c++ code (which is easy enough to turn into python).
The question I have is: How much are you doing this?
Is this something that’s going to happen a handful of times per frame? Or just once for a script? Then write a function that works, and don’t try to make it faster until you’re done, and you profile your code, and find out that’s the slow part.
Or is this something where you’re projecting every point on one mesh to every edge on another? Where you’re planning on thousands, or hundreds of thousands of operations? In which case, optimizing it might actually be called for. And for things like that, numpy is your friend. You’d still write basically the same thing, you’d just use numpy’s built-in functions to do each step on multiple lines at once.
For each point n0 along the line [p1:p2] get the projected point n1 on the line [p3:p4]. Project n1 back against [p1:p2] and test if it is the same value as n0. Roughly something like this:
for i in range(1.0/1000):
p1_p2_normal = (p2-p1).normal()
p3_p4_normal = (p4-p3).normal()
n0 = (1-i) * p0 + p1 * i
n1 = (((n0-p1) * p3_p4_normal) * p3_p4_normal) + p3
n2 = (((n1-p2) * p1_p2_normal) * p1_p2_normal) + p1
if n2 == n0:
break
# or
if 0.0 < (n2-n0).length() < minima:
break
If this [n0:n1] distance is zero - the lines are intersecting. You’d have to test for no valid results. This could also be a while handle - moving back and forth until a minima is met. Else you might need lots of iterations.
This would, of course, work. And if you were trying to be fancy, you could even do a binary search instead of a linear one.
# I'm assuming some functions are defined:
# project_distance() projects a vector onto a unit vector, and gets the distance
# between the vector and it's projection.
# Could be optimized to return the squared distance
# project_point() projects a vector onto a unit vector, and returns the projected point
# distance() finds the euclidean distance between two points.
# Could be optimized to return the squared distance
# addition and subtraction are defined between points/vectors
# multiplication and division are defined between points/vectors and scalars
def closest_on_skew(p1, p2, p3, p4, tol=0.00001):
p1_p2_normal = (p2-p1).normal()
p3_p4_normal = (p4-p3).normal()
# Subtract p3 out from the check points. Because if we do this relative to p3
# then it simplifies a lot of the math, and we can just add it back in later
# This is an easy optimization, so long as it's commented
c1 = p1-p3
c2 = p2-p3
c1_dist = project_distance(c1, p3_p4_normal)
c2_dist = project_distance(c2, p3_p4_normal)
while distance(c1, c2) > tol:
midpoint = (c1 + c2) / 2
mid_dist = project_distance(midpoint, p3_p4_normal)
if c1_dist > c2_dist:
c1 = midpoint
c1_dist = mid_dist
elif c2_dist > c1_dist:
c2 = midpoint
c2_dist = mid_dist
else:
# They're equal. So the only *possible* cases are that
# the lines are parallel, or the midpoint is the exact
# minimum.
break
# We've either hit tolerance, found parallel lines, or an exact min
# so take one last midpoint and return the points as requested
midpoint = (c1 + c2) / 2
# Don't forget to add p3 back into the mix
return midpoint + p3, project_point(midpoint, p3_p4_normal) + p3
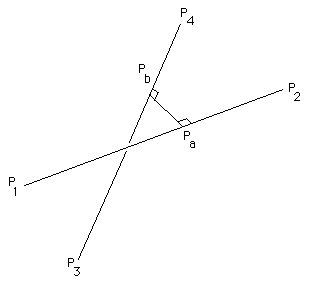
However, since there’s a direct algebraic solution that you can find by solving for this property
dot(n1-n0, p1_p2_normal) == 0 and dot(n1-n0, p3_p4_normal) == 0
(Meaning the shortest segment that connects two skew lines is perpendicular to both of the skew lines)
I would just do the algebra once, and write code for the exact solution
Yes @tfox_TD totally! Wikipedia has a good page on this: Skew Lines
The cross product of the two lines (norm) can test if the lines are parallel - which you can fallback to just getting the distance between the first point of each line:
d0 = (p1 - p0).normal()
d1 = (p3 - p2).normal()
c0 = p0
c1 = p2
n = d0 ^ d1
if n.length():
n0 = d0 ^ (d1 ^ d0)
n1 = d1 ^ n
c0 = p0 + (((p2 - p1) * n1) / (d0 * n1)) * d0
c1 = p2 + (((p1 - p2) * n0) / (d1 * n0)) * d1
return c0, c1